| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 미니 화이트
- 마이크로소프트
- 샤오미
- django
- 탱크램팩토리
- 아이디어팩토리
- restful
- IOT
- virtualenvwrapper
- AWS EC2
- 스마트 러닝화
- ted
- windows
- uWSGI
- PostgreSQL
- nginx
- 온오프믹스
- UserCreatioForm
- 위즈네트
- 데이터 이전
- Python
- psycopg2
- 무브나우
- help_text
- berkeley db
- 워크샵
- LED
- 미밴드 1S
- virtualenv
- 스포츠코치
- Today
- Total
NERD WORLD
컴퓨터과학이 여는 세계(이광근) - P/NP 문제 본문
서울대학교 컴퓨터공학부 이광근 교수님이 쓰신, '컴퓨터과학이 여는 세계' 라는 책을 읽고 있다. 총 5장 중에서 4장 중반까지 읽었는데, 정말 훌륭한 교양 과학서라 생각한다. 책을 읽다보면 컴퓨터과학의 중요한 주제들이 연달아 등장한다. 이 중에서 블로그 포스트로 정리하고, 이해를 다져놓고 싶은 부분들에 대해서 간단히 정리한 것이다. 이 포스트로 해당 주제를 처음 접하는 사람을 위하기보다는, 내 자신의 이해를 다지기 위한 목적으로 포스트를 작성해볼 것이다.
이번 포스트의 주제는 'P = NP 문제' 이다. 컴퓨터과학에서 매우 중요한 문제 중 하나이다. 이 문제를 푼다면, 아마 컴퓨터과학계의 노벨상이라 불리는 튜링상은 따논 당상 아닐까....
용어 정의를 통해서 개념을 잡아보도록 하자. 컴퓨터로 풀 수 있는 문제들(questions)을 몇개의 종류로 분류할 것이다.
P : 문제를 풀 수 있는 다항식 시간 복잡도(polynomial time-complexity)의 알고리즘이 존재하는 문제들을 class P 혹은 그냥 P 라고 분류한다.
NP : 답이 주어졌을 때(맞는 답인지는 모르는, 답의 후보군), 이 답이 문제의 올바른 답인지 여부를 판단할 수 있는(verified) 다항식 시간 복잡도(polynomial time-complexity)의 알고리즘이 존재하는 문제들을 NP 라고 분류한다. NP는 Nondeterministic polynomial time 의 약자이다.
P와 NP의 정의에 의해서, NP 문제들의 집합이 P 문제들의 집합을 포함한다는 것을 알 수 있다. 다항식 시간내에 답을 구할 수 있는 문제는, 당연히 다항식 시간내에 제시된 답이 올바른지 여부도 판단할 수 있을 것이다.
NP 문제라는 집합으로부터, 2개의 추가적인 문제 집합이 파생된다. 아래에 서술된 NP-complete와 NP-hard가 그들이다.
NP-hard : 모든 NP 문제들이 자기 자신으로 다항식 시간내에 환원될 수 있다면, 그 문제들을 NP-hard 라고 한다. 쉽게 표현하자면, 어느 NP-hard 문제 하나라도 다항식 시간내에 풀리는 알고리즘이 발견된다면 모든 NP 문제들이 다항식 시간내에 풀릴 수 있으므로 NP = P 가 성립한다. NP 문제를 NP-hard 문제로 환원하고, NP-hard 문제를 풀고, 그 NP-hard 문제의 답을 다시 NP 문제의 답으로 적절히 환원하는 세 가지 과정이 모두 다항식 시간내에 가능하므로 전체 과정이 다항식 시간 복잡도를 가지기 때문이다.
NP-complete : NP-hard 문제들 중에서, NP 이기도 한 문제들을 NP-complete 라고 한다. 즉, 일반적으로 NP-hard 문제는 NP 하지 않을 수 있다. 그러니 그 중에서 NP 이기도 한 문제들을 따로 NP-complete 라고 분류한 것이다. NP-complete 는 NP 집합에 속하면서, 또한 그 중 하나라도 다항식 시간 복잡도의 알고리즘이 발견된다면 모든 NP 집합의 문제들의 다항식 시간 복잡도의 알고리즘이 찾아지기 때문에 NP 집합의 문제들이 '완전히' P 집합에도 속하게 된다. 그런 맥락에서 'complete' 라는 단어를 덧붙인 것이다.
NP-complete 문제들 중 어느 하나라도, 그 문제를 푸는 다항식 시간 복잡도의 알고리즘이 개발된다면 모든 NP 문제들은 다항식 시간내에 풀릴 수 있으므로 "P = NP 문제" 는 답이 Yes 인 것으로 풀리게 된다.
NP 문제들은 컴퓨터로 '이론적으로는' 풀 수 있지만, 그 시간 복잡도가 지수함수적이므로 현실적으로 풀 수 없어 보인다. 그런 거대한 NP 문제들의 집합이, 단 하나의 NP-complete 문제(혹은 NP-hard 문제도 마찬가지다. 필자 개인의 근거없는 추측으로, NP-hard 문제보다는 NP-complete 문제가 그나마 쉽지 않을까 하는 생각이다)만 풀린다면 연쇄적으로 모두 풀린다는 사실이 무척이나 흥미롭다. 이런 연쇄작업의 기틀을 마련해준 사람이 바로 스테픈 쿡(Stephen Cook)이다. 쿡이 찾은 최초의 NP-complete 문제가 바로 Boolean satisfiability problem 이다. 이는 1971년도에 출간된 논문에 Cook-Levin theorem 으로 제시되어 있다. 현대 컴퓨터 동작원리에 근간을 이루는 튜링머신(Turing machine)의 개념으로부터 파생되는 태초의 NP-complete 문제가 있고, 이를 최초로 자연스러운 문제(natural problem)의 형태로 기술한 사람이 쿡이라고 이해하면 될 것이다. 여담이지만 이 업적으로 쿡은 1982년도에 튜링상을 수상하였다.
마지막으로, 영문 위키피디아에서 P, NP, NP-hard, NP-complete 집합의 포함관계를 잘 나타낸 다이어그램이 있어 이를 첨부한다.
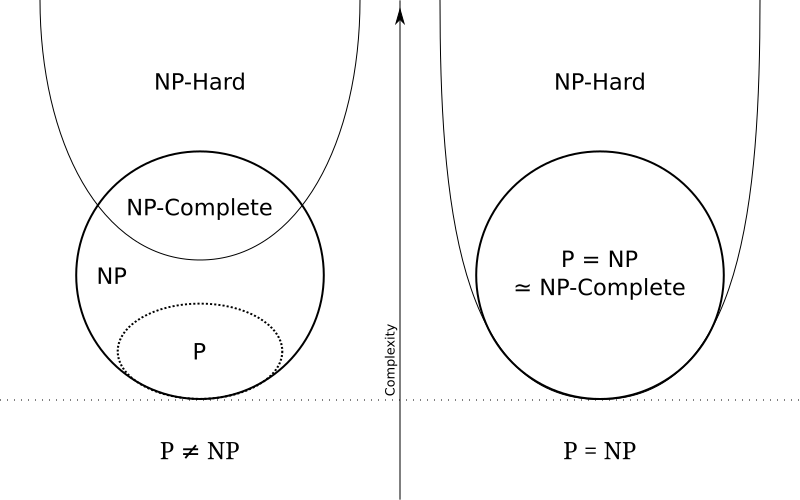
출처 :
'일상' 카테고리의 다른 글
| WIZnet 4월 아카데미 - IoT 디바이스 컨트롤을 위한 쉬운 스마트폰 APP 활용 (1) (2) | 2016.04.18 |
|---|---|
| 작은누나 생일선물 (0) | 2016.04.16 |
| 아이디어팩토리 - 아두이노 워크샵 (0) | 2016.03.29 |
| 아이디어팩토리 - 3D 프린터 워크샵 (3) | 2016.03.25 |
| 마이크로소프트 멜팅팟 세미나 - "응답하라 Python!!" (0) | 2016.03.24 |




